سرفصل و موضوعات تدریس ریاضی یک عمومی دانشگاهی

تابع 

شامل موارد زیر است:

حاصلضرب دکارتی - رابطه - تابع - دامنه تابع - تساوی دو تابع - ترکیب دو تابع - توابع زوج و فرد - تابع یک به یک - تابه معکوس - توابع چند

جمله ای - توابع مثلثاتی - توابع لگاریتمی - تابع نمایی - توابع هیپربولیک - برد تابع - تابع پوشا - تابع متناوب 

حدو پیوستگی 

محاسبه حد از روی ضابطه - محدودیت های حدی - قضایای حدی - صورت های مبهم حدی - حالات مبهم - رفع ابهام - حالات مبهم 

مرکب - رفع ابهام صفر در بی نهایت - حالت مبهم بینهایت منهای بی نهایت - رفع ابهام حالات مبهم نمایی - پیوستگی تابع در نقطه x - 

انواع ناپیوستگی - پیوستگی روی بازه - مجانب ها 

در عنوان بعدی ادامه مباحث ذکر میشود 

قضیه لاگرانژ یا مقدار میانگین

مشتق و مطالب مرتبط با ان نقش مهمی در ریاضیات ایفا میکند اما کاربرد قضیه لاگرانژ یا مقدار میانگین و نتایج آن در حل مسائل ریاضیات مقدماتی همیشه مهم بوده است 

اثبات اتحاد ها نامساوی ها و فرمول های مثلثاتی و تبدیل عبارتهای جبری به حاصل ضرب و حل معادله و نامعادله و دستگاه معادله و معادله های پارامتری با استفاده از این قضیه امکان پذیر است.

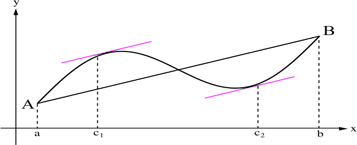
صورت کلی قضیه لاگرانژ 

اگر تابع f  در بازه [a,b] پیوسته باشد و در تمام نقاط بازه (a,b)  مشتق پذیر است آنگاه در این بازه نقطه ای مانند c وجود دارد به طوری که رابطه زیر برای آن برقرار است 

مشتق تابع در نقطه c  برابر است با مقدار تابع f  در نقطه b  منهای مقدار تابع در نقطه  a تقسیم بر تفریق مقدار b  با  a

 نتایج سه گانه از این تعریف و قضیه به شرح زیر میباشد:

1 - به شرط اینکه تابع ما ثابت باشد اگر تابع f  در بازه [a,b] پیوسته و مشتق آن در داخل این بازه صفر باشد انگاه تابع در بازه [a,b] ثابت است.

2- اگر دو تابع f و g  در بازه [a,b]  پیوسته باشند و در داخل این بازه مشتق های مساوی داشته باشند اختلاف آنها تنها در مقادیر ثابت خواهد بود.

3- اگر تابع ما یکنوا باشد و تابع f  در بازه ای دلخواه مانند I  پیوسته و مشتق آن در آن بازه مثبت و یا منفی باشد ان گاه تابع f  در این بازه صعودی و یا نزولی است. 

کاربرد مشتق

ما معمولا در هنگام مطالعه مشتق به مبحثی تحت عنوان کاربرد مشتق میرسیم که در اینجا من میخواهم به 11 مورد از مهمترین کاربر

 های مشتق اشاره نمایم و در مطالب آینده در خصوص هر یک توضیحات و مطالبی ارائه دهم 

معمولا کاربرد مشتق در موارد زیر متداول میباشد

1- بدست آوردن خط مماس و قائم بر یک منحنی در نقطه ای بر روی منحنی

2- تعیین زاویه حاده بین دو منحنی

3- استفاده در قضایای رل و لاگرانژ موسوم به قضیه مقدار میانگین

4- بدست آوردن مقدار تقریبی و تقریب خطی

5- بدست آوردن نقاط بحرانی در نمودار یک تابع

6 - بدست آوردن اکسترمم های نسبی و آزمون های مشتق اول و مشتق دوم

7- بدست آوردن نقاط عطف بر روی منحنی

8 - بحث تحلیلی اهنگ تغییرات بر روی تابع

9- بدست آوردن اکسترمم های مطلق و بهینه سازی

10 - محاسبه فرایند رشد و زوال 

11- تعیین تعداد ریشه های یک معادله

ساعات حضوری برای تدریس در طول هفته

بسمه تعالی

به اطلاع دوستان و دانش آموزان و دانشجویان عزیز میرساند برای ارائه خدمات آموزشی 

خصوصی و نیمه خصوصی در ماه جاری ساعات زیر برای همکاری و آموزش در نظر گرفته 

شده است که به شرح زیر میباشد در خصوص هزینه تدریس به صورت خصوصی و نیمه 

خصوصی و شرایط مربوطه به لینک تعرفه آموزشی مراجعه فرمایید .  با تشکر 

یکشنبه  ساعت 18 الی 22 

دوشنبه  ساعت 18 الی 22

سه شنبه ساعت 18 الی 22

پنج شنبه ساعت 17 الی 22

جمعه ساعت 10 الی 22

این تاریخ های ذکر شده تا انتهای آبان ماه قابل استناد میباشد و برای ماه جدید متعاقبا اعلام میگردد.