آشنایی با نرم افزار آنلاین حل مسائل ریاضی

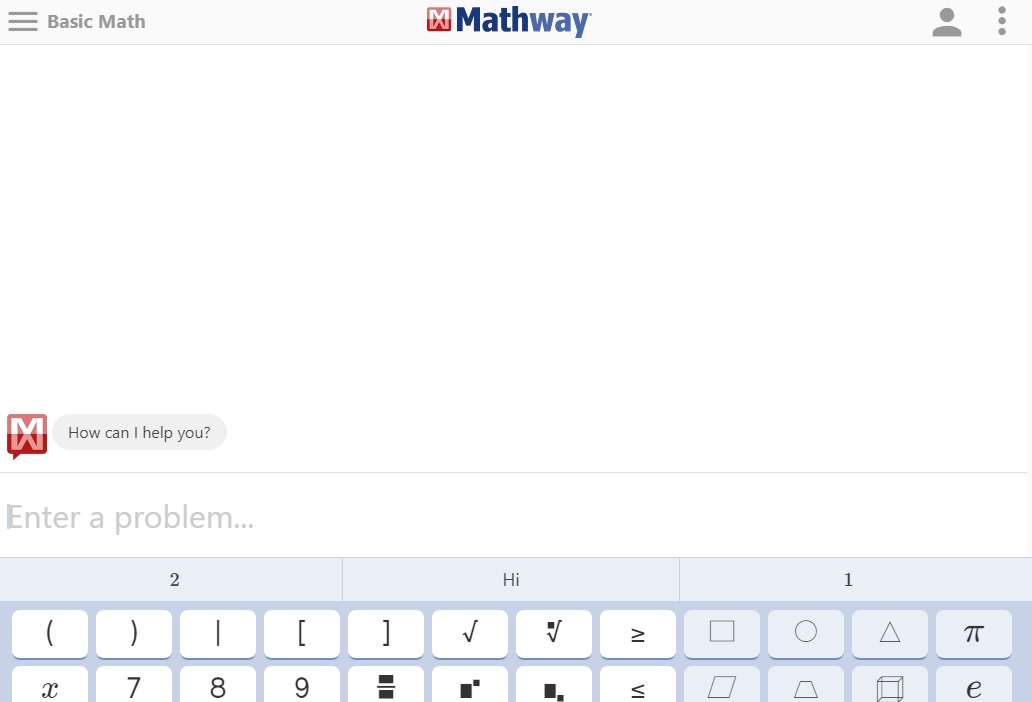
امروز قصد دارم شما را با یکی از نرم افزارهای تحت وب قدرتمند و انلاین حل مسائل ریاضی با نام mathway آشنا کنم به جرات میتوان گفت این نرم افزار نیاز هر یک از افراد را در مباحث مختلف ریاضی برطرف میکند برای استفاده از این نرم افزار لازم است ابتدا به سایت این نرم افزار به آدرس https://www.mathway.com مراجعه نمایید 

پس از باز شدن سایت صفحه ای برای شما نمایان میگردد . در گوشه سمت چپ شما یک منو با عنوان calculus میبینید که اگر بر روی ان کلیک نمایید منویی باز میشود که به صورت موضوع بندی برای شما مباحث ریاضی را دسته بندی کرده که به ترتیب معادل فارسی آنها به شرح زیر میباشد :

basic math ..... ریاضی پایه

pre algebra .... جبر پایه

algebra ...... جبر 

trigonometry .....  مثلثات

precalculus ...... حساب دیفرانسیل مقدماتی

calculus ........ حساب دیفرانسیل و انتگرال

statistics ...... آمار

finite math.....  ریاضیات گسسته

linear algebra ...... جبر خطی

chemistry ...... شیمی

graphing ...... نمودار

این نرم افزار این قابلیت را دارد که شما میتوانید معادله را وارد کرده و بلافاصله نمودار آن را رسم نماید

امیدوارم از این نرم افزار لذت ببرید و مشکلات بسیاری را برای شما هموار نماید .

نمایش متحرک از نحوه تشکیل مقاطع مخروطی

در این انیمیشن ما به صورت روشن نحوه بوجود آمدن مقاطع 4 گانه مخروطی را در هنگام تقاطع یک صفحه با مخروط دو سر را مشاهده میکنیم.

 

 

سرفصل های تدریس درس حساب دیفرانسیل و انتگرال دوره پیش دانشگاهی

مفاهیم اعداد 

دنباله ها و سریها

حدو پیوستگی

مشتق و کاربرد آن

انتگرال و کاربرد آن

سرفصل های تدریس درس حسابان پایه یازدهم

سرفصل تدریسی به صورت تفکیک شده به شرح زیر میباشد 

 دنباله های حسابی و هندسی

معادلات درجه دوم

معادلات گویا و گنگ 

قدرمطلق

توابع و انواع آن

اعمال بر روی توابع

مثلثات

حد و پیوستگی

لازم به ذکر است هر یک از گروه های نام برده شده دارای زیر فصل و عناوین جزئی تر میباشند 

مقطع مخروطی چیست؟

قبل از هر چیز بهتر هست این سوال را از خود بپرسیم دانستن اشکال مخروطی و پیچیدگی این اشکال چه فایده ای برای ما خواهد داشت برای پاسخ به این سوال بهتر است ابتدا با این اشکال بیشتر اشنا شویم 

قبل از هر چیز من به یکی از این کاربرد ها اشاره میکنم . ما میداینم که در مکانیک اجرام در حوزه اختر شناسی  و در مساله دو جسم، هر جسمی که تحت اثر گرانش جسمی دیگر قرار داشته باشد  در مسیری حرکت میکنه که قسمتی از یک مقطع مخروطیه حال ما لزوما برای بررسی اثرات گرانشی اجرام بر هم باید سطح اثر و دامنه شکل اثر را کاملا محاسبه نماییم 

در صورت کلی میتوان گفت مقاطع مخروطی عبارتند از منحنیهای دو بعدی که در اثر برخورد یک صفحه با مخروطی توخالی به وجود می آید.(معمولا دو مخروط که از راس به هم چسبیده اند و هم محورند به نمایش در می آیند). نمونه ای از این حالت در شکل زیر بیان شده است .

بر حسب این که برخورد صفحه با مخروط ها  چگونه باشد اشکال زیر تولید می شود.

1- دایره(قرمز): صفحه برخوردی عمود بر محور مخروط باشد.
2-بیضی(زرد): زاویه برخورد صفحه مایل باشد و یک سطح محصور ایجاد نماید 
3- سهمی(آبی): صفحه برخوردی به صورت موازی با یال یا سطح جانبی مخروط باشد. در واقع سهمی مسیری باز است که فقط در یک مخروط ایجاد میشود.
4-هذلولی(سبز): زاویه برخورد صفحه به گونه ای باشد که دو مسیر باز در دو مخروط ایجاد شود. 

 این موارد بیان بسیار ساده از این اشکال فضایی مهم بوده اند که امیدوارم مفید بوده باشد در پست های بعدی هر یک از این موارد 4 گانه را به صورت کامل و شفاف و با بیان ساده بررسی خواهیم کرد تا به اهمیت وجود این اشکال در علوم پایه جدید پی ببرید .

تعرفه ها و هزینه های آموزشی

لیست تعرفه های آموزشی 

انتگرال چیست؟

به نام خدا

در این قسمت مطلب مختصری در خصوص انتگرال خدمت شما ارائه میدهم

دوستان عزیز ما همواره وقتی یک تابع مانند y=x³+4x²+5x-7  دانشته باشیم  و بگوییم از این تابع مشتق بگیرید حاصل عبارت میشود :

3x²+8x+5  حال اگر ما در جایی قرار گرفتیم که مشتق را داشتیم و خواستیم تابع اولیه را بدست آوریم را عمل تابع اولیه گیری را انجام میدهیم  برای بدست اوردن این تابع اولیه روشمان را اصطلاحا انتگرالگیری مینامند.

حال شاید از شما سوال شود تاریخچه و علل بوجود آمدن این مکانیزم چه بوده است؟

در واقع میتوان گفت 5 نفر در تاریخ در ارائه و پیشبرد و خلق این موضوع در ریاضیات نقش پررنگی داشتند که عباتند از :

لایب نیتس

نیوتن

فوریر

گائوس

لیوویل

ریمان

عقیده لایب نیتز و نیوتن این بود که مشتق و انتگرال یکدیگر را خنثی میکنند و با استفاده از این ارتباط توانستند بسیاری از مسائل هندسی و نجومی را حل نمایند.

گائوس اولین نفری بود که جداول انتگرال را نوشت و میتوان گفت تلاش وی باعث ورورد بیش از پیش انتگرال به حوزه فیزیک شد

ریمان اولین فردی بود که توانست انتگرال معین را بر اساس یافته های معین و مستدل و منطقی استوار کند.

نکته دیگر اینکه نماد هایی که در محاسبات دیفرانسیل و انتگرال میبینیم همگی بوسیله لایب نیتس ابداع شده اند. 

 در اینجا لیست جدول انتگرال را که به کوشش گائوس ایجاد شد را خدمت شما ارائه میدهم که بسیار کاربردی و مفید است .

جدول انتگرال 

معادلات دیفرانسیل و کاربرد آن

با نام خدا

در ادامه بحث ممکن است شما دوستان عزیز این سوال برایتان پیش بیاید که اصلا کاربرد و فلسفه معادلات دیفرانسیل چیست؟ این سوال به جا را اینگونه تحلیل میکنیم که ما در زندگی و مخصوصا مباحث حرکتی و اصطلاحا دینامیکی در طبیعت به پدیده هایی برمیخوریم که در آنها برای بدست اوردن یک عامل احتیاج به تغییرات عامل دیگر داریم مثلا در پدیدیه فشار بر سطح عامل ارتفاع عاملی مهم در میزان فشار است به عبارتی فشار برای تغییر همواره وابسته با ارتفاع است و به عبارتی گفته میشود پارامتر ارتفاع همواره متغیری مستقل میباشد و فشار متغیری وابسته هست و به نحوه دیگر وابسته به ارتفاع . حال این پدیده در عواملی مثل حرکتهای متغیر شتابدار بسیار کاربرد دارد و یک معادله دیفرانسیل همواره از یک متغیر مستقل x  و متغیر وابسته y  و مشتات مراتب مختلف این متغیر وابسته تشکیل شده است . در واقع میتوان گفت تغییرات متغیر y  وابسته به تغییرات متغیر x میباشد . پس در هر مرحله ما برای اینکه تشخیص دهیم آیا معادله ای دیفرانسیل هست یا نه باید ببینیم آیا در معادلع متغیر وابسته غ به همراه مشتقاتش موجود هست یا خیر 

ودر حالت کلی میتوان گفت معادله دیفرانسیل یک معادله بین تابع و مشتقات تابع نسبت به متغیر مستقل x میباشد و در اینجا منظور از تابع  y میباشد.

معادلات دیفرانسیل چیست؟ قسمت سوم

به نام خدا

در قسمتهای قبل به بررسی ساختارهای یک معادله پرداختیم در اینجا میخوام به صورت کلی معادلاتی را که میشناسیم را بررسی نمایم

دسته اول معادلات که همگی با آن آشنایی داریم معادلات یک مجهولی هستند که با نماد  0=(f(X نمایش میدهند و دسته دیگر معادلات یک مجهولی درجه دو هستند یعنی معادلاتی که توان مجهول 2 میباشد و با نماد 0 = (f(X² نمایش داده میشود .

پاره ای دیگر از معادلات معادلاتی با دو مجهول x و y  میباشند و در معادله مورد نظر دو مجهول نمایان هستند که شکل نمایشی به صورت یک زوج مرتب با علامت f میباشد 0 = (f(x,y

 و این نوع معادله زمانی که توان دو مجهول x و y یک باشد معادله دومجهولی درجه یک و اگر توان آنها دو باشد معادله دو مجهولی درجه دو نام دارد.

نهایتا ما به نوع دیگری از معادلات برمیخوریم که در انها مجهول هایی داریم که در کنار آنها در عین اینکه ممکن است دارای توان باشند مشتقات انها نیز در معادله ظاهر شده باشد . یعنی ممکن است مشتقات اول و یا دوم این متغیر ها در معادله دیده شود به طور کلی میتوان گفت معادلاتی که در آنها تعداد متناهی از مشتقات متغیر وجود داشته باشد معادله دیفرانسیل میگوییم. در اینجا ذکر نکته ای حائز اهمیت است و اینکه در این معادلات معمولا دو نوع متغیر وجود دارد که اصطلاحا یکی وابسته و دیگری مستقل میباشد که در مطالب بعدی انها را شرح خواهیم داد.

معادلات دیفرنسیل چیست ؟ قسمت دوم

به نام خدا 

در ادامه مطلب قبل در خصوص فلسفه معادلات دیفرانسیل بهتر است بحث را به این صورت آغاز کنیم که بگوییم معادلات به طور کلی چیست ؟

معادله را به جرات میتوان گفت همه ما میدانیم و حتی به صورت غیر مستقیم در زندگی روزمره استفاده میکنیم در حالت کلی و صوری میتوان گفت معادله یعنی یافتن مجهول 

در قالب زبان ریاضی میتوان گفت که معادله یک رابطه است که در آن همواره علامت تساوی (=) وجود دارد و همواره در یک معادله مقادیر 

مجهولی وجود دارد که این مقادیر به ازاء مقادیر خاص و مشخصی در معادله صدق میکنند اینجا مفهوم صدق کردن یعنی اینکه اگر ان عدد ها 

در معادله قرار دهیم دو طرف تساوی با هم برابر خواهد شد . به طور کلی در برخورد با معادلات همواره دو سیاست را به کار میبریم یا اینکه یک دسته اعداد در اختیار داریم یعنی مجموعه ای از اعداد که به احتمال زیاد جواب در انهاست و لذا یکی یکی آنها در معادله و جایگاه مجهول قرار مجهول قرار میدهیم که اصطلاحا صدق کردن نامیده میشود و حالت دوم روش عملیاتی برای بدست آوردن جواب میباشد که در حالت کلی مقادیر معلوم در یک طرف تساوی و مقادیر مجهول در طرف دیگر قرار گرفته و مقادیر معلوم بر ضرایب مجهول تقسیم میشود و جواب این تقسیم مسلما جواب معادله میباشد .

در دنیای ریاضی ما معادلات را معمولا بر اساس تعداد مجهول طبقه بندی میکنیم و در یک تقسیم بندی دیگر بر اساس نوع پارامتر های استفاده شده در معادله طبقه بندی میکنیم .